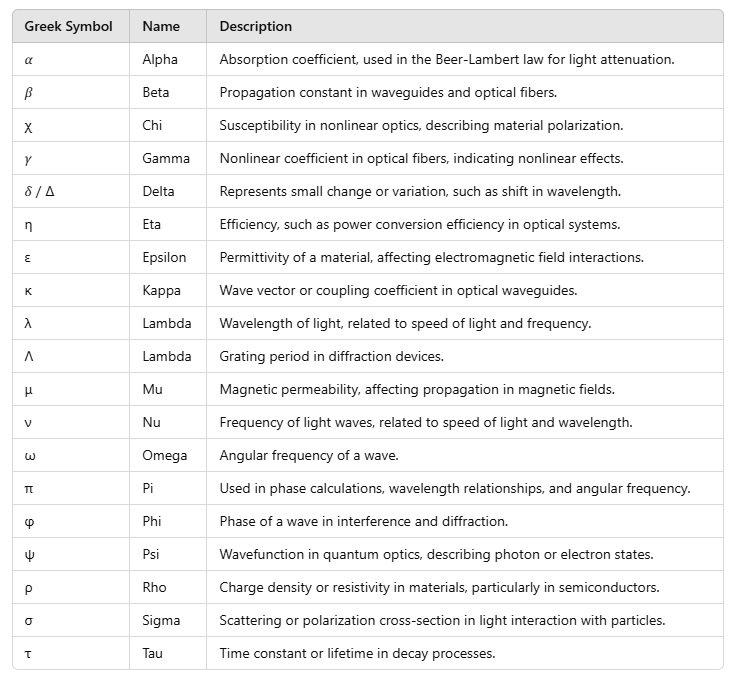
The Greek alphabet is conventionally used in photonics to represent multiple physical quantities, variables and constants. Greek letters represent an internationally comprehended language in which many important physical quantities and variables are represented. It provides clarity and consistency in communicating research papers, technical documents, and lectures all over the world.
In the time of Greek philosophers, the letters and symbols used to denote physical properties and constants were thus supplied by such ancient Greek mathematicians and scientists as Euclid and Archimedes. Over time, Greek symbols conventionally became universally accepted to stand for certain constant values or physical properties, hence universalizing the language of the sciences and engineering.
The following is a list of Greek letters most commonly applied in photonics, along with their meanings and explanations.
Alpha (𝛼)
Often represents the absorption coefficient in materials, indicating how much light is absorbed per unit length in a material. It is used in the Beer-Lambert law to describe the attenuation of light passing through a medium:
\( I = I_0 e^{-\alpha x} \)
Beta (𝛽)
Represents the propagation constant or phase constant in waveguides and optical fibers, crucial for understanding waveguide modes. Calculated as:
\( \beta = \frac{2\pi}{\lambda} n_{\text{eff}} \)
Chi (χ)
Represents susceptibility in materials, especially in nonlinear optics where it describes material polarization response to an electric field.
\( P = \chi E \)
Gamma (𝛾)
Denotes the nonlinear coefficient in optical fibers, indicating the strength of nonlinear effects:
\( \gamma = \frac{2 \pi n_2}{\lambda A} \)
Delta (𝛿) or (Δ)
Often represents a small change or variation, such as a shift in wavelength:
\( \Delta \lambda = \lambda – \lambda_0 \)
Eta (η)
Often represents efficiency, such as power conversion efficiency in optical systems.
\( \eta = \frac{\text{Output Power}}{\text{Input Power}} \)
Epsilon (ε)
Represents the permittivity of a material, critical in electromagnetic field interactions:
\( \varepsilon = \varepsilon_r \varepsilon_0 \)
Kappa (κ)
Represents the wave vector or coupling coefficient in optical waveguides. The wave vector \( \kappa \) is used in wave propagation, especially in optical fibers and waveguides, and is related to photon momentum in a medium.
\( \kappa = \frac{2 \pi}{\lambda} n_{\text{eff}} \)
Lambda (λ)
Represents the wavelength of light, related to the speed of light and frequency:
\( \lambda = \frac{c}{f} \)
Lambda (Λ) – Uppercase
Denotes the grating period in diffraction devices. The grating period \( \Lambda \) is the distance between grooves on the grating, determining diffraction angles.
\( \Lambda = \frac{\lambda}{\sin \theta_m} \)
Mu (μ)
Represents the magnetic permeability, affecting magnetic field propagation:
\( \mu = \mu_r \mu_0 \)
Also used for magnetic permeability or refractive index in nonlinear optics and waveguides.
\( \mu = \frac{1}{\epsilon} \)
Nu (ν)
Denotes the frequency of light waves, relating to the speed of light \( c \) and wavelength \( \lambda \).
\( \nu = \frac{c}{\lambda} \)
Omega (ω)
Represents the angular frequency of a wave:
\( \omega = 2 \pi f \)
Pi (π)
Used in phase calculations, wavelength relationships, and angular frequency.
\( \omega = 2 \pi f \)
Phi (φ)
Represents the phase of a wave in interference and diffraction:
\( E = E_0 \cos(kx – \omega t + \varphi) \)
Also used to represent the potential function or electric potential in wave propagation.
\( \varphi = \omega t – kx \)
Psi (ψ)
Represents the wavefunction in quantum optics, describing photon or electron states.
\( |\psi\rangle = \sum_n c_n |n\rangle \)
Rho (ρ)
Used for charge density or resistivity in materials, particularly in semiconductors and photonics.
\( \rho = \frac{1}{\sigma} \)
Sigma (σ)
Represents scattering or polarization cross-section in light interaction with particles or molecules.
\( \sigma = \frac{8 \pi}{3} \left(\frac{d}{\lambda}\right)^4 \)
Tau (τ)
Represents the time constant or lifetime in decay processes.
\( I(t) = I_0 e^{-\frac{t}{\tau}} \)
Theta (θ)
Commonly represents the angle in equations like Snell’s law:
\( n_1 \sin(\theta_1) = n_2 \sin(\theta_2) \)
Also representes angles in diffraction, reflection, and refraction processes.
\( d \sin(\theta) = m \lambda \)
Upsilon (Υ)
Denotes quantum yield or efficiency in photon emission processes like fluorescence.
\( \Upsilon = \frac{\text{Number of emitted photons}}{\text{Number of absorbed photons}} \)
Xi (ξ)
Represents electric susceptibility, a measure of material response to an electric field.
\( \mathbf{P} = \varepsilon_0 \chi_e \mathbf{E} \)
Zeta (ζ)
Used for the attenuation coefficient or damping factor in resonant systems.
\( \zeta = \frac{c}{2} \sqrt{\frac{\sigma}{m}} \)
Table of Greek Symbols from Greek Alphabet used in Photonics
